Sabemos que es muy complicado de que un sistema eléctrico esté completamente equilibrado, sien lo lo más común de que tenga cierto desequilibrio de corrientes.
Como consecuencia de dicho desequilibrio de corrientes, en un sistema trifásico de cuatro hilos, 3 fases más neutro, el retorno de la corriente de desequilibrio se produce precisamente a través del conductor de neutro.
Pero, ¿Cómo podemos determinar la corriente de neutro si solo conocemos las corrientes de fase?
En este artículo te explicaré como calcular la corriente de neutro con UNA SOLA FORMULA!!!
NOTA:
- Esta formula no tiene en cuenta el efecto de retorno de los armónicos eléctricos múltiples de tres.
- Solo es aplicable cuando el desfase entre las tres corrientes de fase es de 120º entre ellas.
Tabla de contenido
Fórmula para cálculo rápido de la corriente de neutro
Para no liarnos, primero vamos a representar un esquema básico eléctrico:

En este ejemplo tenemos 250 A en la línea L1, 180 A en la línea L2 y 140 A en la línea L3, y desconocemos la corriente de retorno en el neutro.
Para que sea menos complicado la demostración de donde sale la fórmula, he sustituido el nombre de la línea L1, L2 y L3 por «A», «B» y «C» respectivamente.
Y ahora … la FÓRMULA:

por tanto, sustituyendo los términos por los valores del ejemplo obtenemos una corriente de neutro de 96,44 A
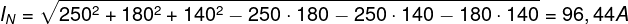
Así de rápido y fácil.
Demostración del origen de la fórmula
Perfecto!!! Es rápida y sencilla, pero puedes pensar, ¿De donde sale esta fórmula?
Voy a explicarte de donde sale paso a paso.
Sistema de fasores
Primero debemos tener el sistema de fasores que conforman las tres corrientes de fase:
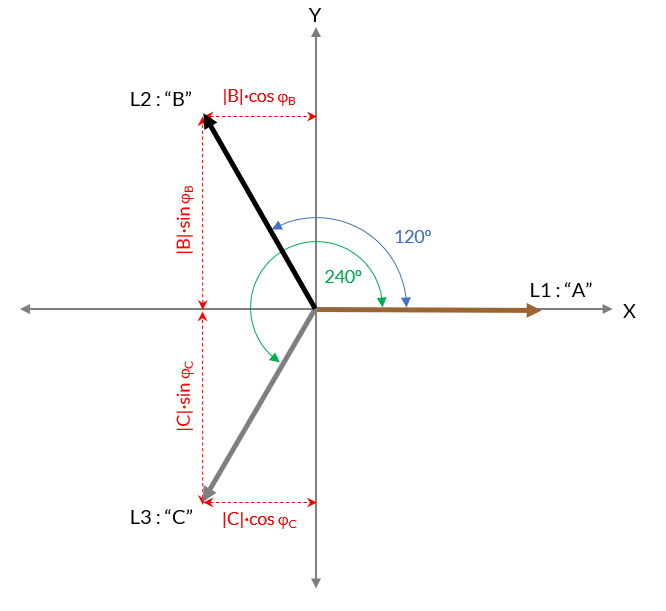
de este sistema obtenemos las componentes cartesianas de los fasores de corriente:
| Corriente | Componente X | Componente Y |
|---|---|---|
| A | A·cos φA | A·sin φA |
| B | B·cos φB | B·sin φB |
| C | C·cos φC | C·sin φC |
En el sistema representado los ángulos φA , φB y φC son 0º, 120º y 240º respectivamente. Con lo que cada componente cartesiana queda:
| Corriente | Componente X | Componente Y |
|---|---|---|
| A | A·cos 0º = A | A·sin 0º = 0 |
| B | B·cos 120º = -B/2 | B·sin 120º = (√3/2)·B |
| C | C·cos 240º = -C/2 | C·sin 240º = – (√3/2)·C |
Módulo de fasor de corriente de neutro
Ya podemos calcular el módulo de la corriente de neutro

donde la componentes X y Y son:
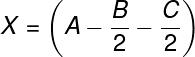

ahora debemos desarrollar X2 y Y2:
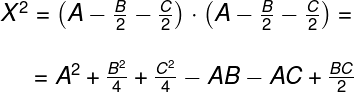
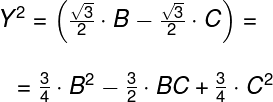
sumamos X2 y Y2
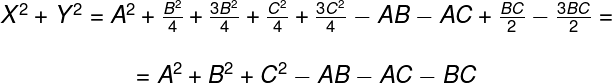
y por último hacemos la raíz cuadrada

vemos que coincide con la formula al inicio del artículo. CORRECTO!!!!
Comprobación del ejemplo
Vamos a comprobar si el resultado obtenido en el ejemplo con la fórmula es el mismo aplicando la descomposición cartesiana.
| Corriente | Componente X | Componente Y |
|---|---|---|
| A=250 A | 250·cos 0º = 250 A | 250·sin 0º = 0 |
| B=180 A | 180·cos 120º = -90 A | 180·sin 120º = 155,88 A |
| C=140 A | 140·cos 240º = -70 A | 140·sin 240º = – 121,24 A |
| N | 90 A | 34,64 A |
por tanto la corriente de neutro será
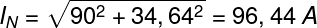
Se confirma que el resultado es el mismo que aplicando la formula simplificada.







