Cuando realizamos ejercicios de trigonométrica o hacemos el cálculo de baterías de condensadores, es habitual realizar los cálculos a partir de unos ángulos predefinidos o más fáciles de recordar.
En este artículo te explicaré la forma más fácil de memorizar las relaciones trigonométricas básicas con la “Regla de la mano izquierda”
Tabla de contenido
Regla mano izquierda
Los ángulos más comunes y más frecuentes que utilizamos son 0º, 30º, 45º, 60º y 90º.
Para recordar las relaciones trigonométricas básicas de estos ángulos, coseno, seno y tangente, solo necesitamos utilizar la “mano izquierda”. Si, si, la mano izquierda.
Ponla delante de ti o sobre la mesa con la palma de la mano hacia ti, el dedo meñique en horizontal y el pulgar hacia arriba, formado 90º. Ya lo tienes, ¡Bien!
Todo lo que debemos recordar a partir de aquí son tres cosas:
- Cada dedo representa un ángulo, de abajo a arriba, seria dedo meñique 0º, dedo anular 30º, dedo corazón 45º, dedo índice 60º y dedo pulgar 90º
- Si seleccionamos un dedo o ángulo, contar cuantos dedos quedan por encima o por debajo. Luego veremos porque
- Y último, recordar la formula √(X)/2
Ahora bien lo bueno …
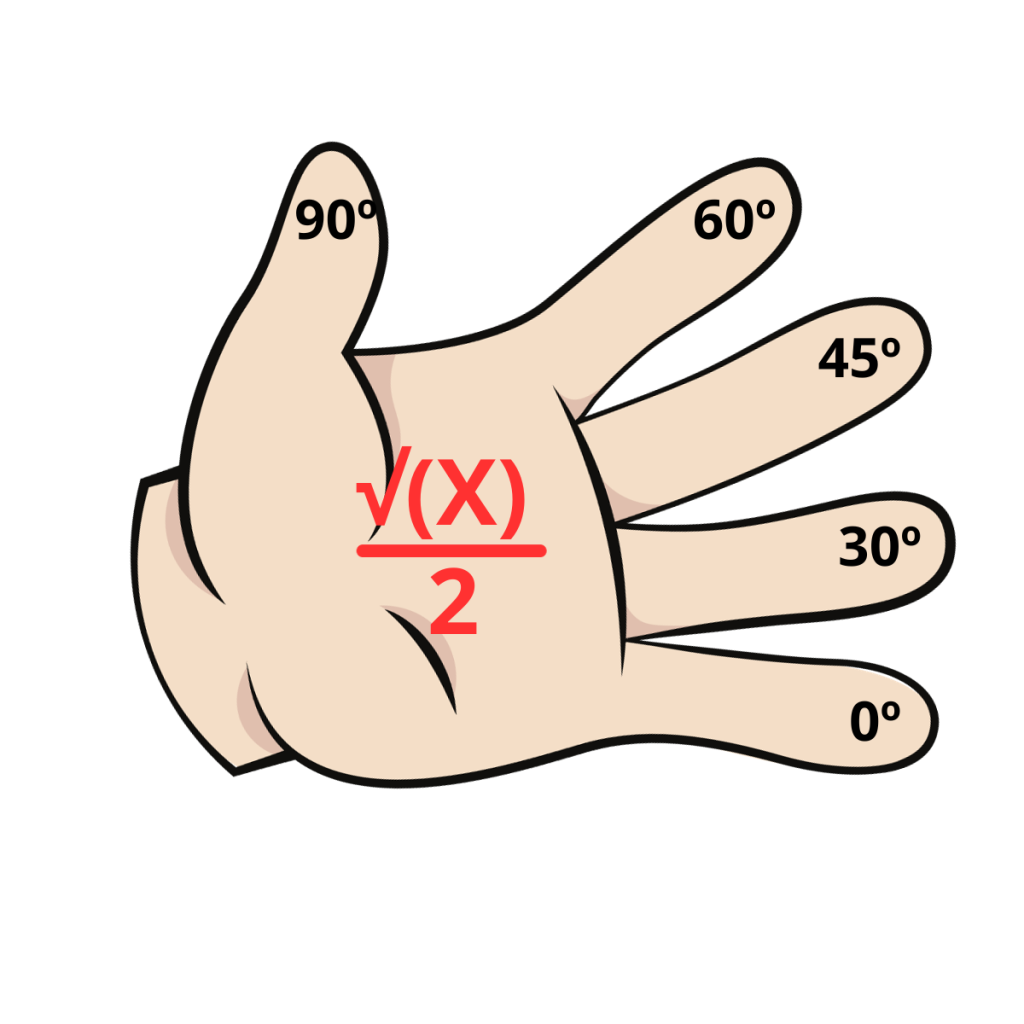
Cálculo seno del ángulo
Vamos a aplicar la regla de la mano izquierda por ejemplo con un ángulo de 30º.
En este caso hemos dicho que el dedo anular es igual a 30º (si te pierdes mira el punto anterior). Lo cerramos y contamos cuantos dedos quedan por debajo. En este caso solo queda 1, que es el dedo meñique.
Aplicamos la formula sustituyendo X por el número de dedos contados. En este caso √(1)/2 . Por tanto el seno de 30º será igual a 1/2.
Si lo repetimos para los otros dedos o ángulos nos queda
| Ángulo | Dedos debajo | Seno ángulo |
|---|---|---|
| 0º | 0 | √(0)/2 =0 |
| 30º | 1 | √(1)/2 =1/2 |
| 45º | 2 | √(2)/2 |
| 60º | 3 | √(3)/2 |
| 90º | 4 | √(4)/2 =2/2 =1 |
Cálculo coseno del ángulo
Ahora vamos a realizar lo mismo que antes para calcular el coseno de un ángulo de 30º.
Volvemos a cerrar el dedo anular, pero ahora contamos los dedos que quedan por encima, que en este caso son 3, corazón, índice y pulgar. ¿te ha salido? !Bien!
Aplicamos la formula sustituyendo X por el número de dedos contados. En este caso √(3)/2 . Por tanto el seno de 30º será igual a √(3)/2
Si lo repetimos para los otros dedos o ángulos nos queda
| Ángulo | Dedos encima | Coseno ángulo |
|---|---|---|
| 0º | 4 | √(4)/2 =2/2=1 |
| 30º | 3 | √(3)/2 |
| 45º | 2 | √(2)/2 |
| 60º | 1 | √(1)/2 =1/2 |
| 90º | 0 | √(0)/2 =0 |
Cálculo tangente del ángulo
Para el cálculo de la tangente partimos de los valores calculados anteriormente del coseno y seno, ya que la tangente será igual a $\tan(x)=\frac{\sin(x)}{\cos(x)}$
Por tanto tenemos que:
| Ángulo | Seno ángulo | Coseno ángulo | Tangente ángulo |
|---|---|---|---|
| 0º | 0 | 1 | 0 |
| 30º | 1/2 | √(3)/2 | 1/√(3) |
| 45º | √(2)/2 | √(2)/2 | 1 |
| 60º | √(3)/2 | 1/2 | √(3) |
| 90º | 1 | 0 | No definida |
Con estas relaciones exactas os ayudará a realizar muchos de los cálculos esenciales que se utilizan en trigonométrica



