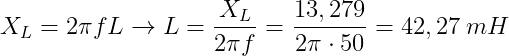Hoy te traigo la resolución de un ejercicio de electrotecnia básico, paso a paso.
Tabla de contenido
Datos de inicio
Nos facilitan los datos de un circuito básico, sabiendo que:

- La tensión es u(t) = 230·√2·cos (2π·f·t) [V]
- La corriente es i(t) = 15·√2·cos (2π·f·t-60º) [A]
- La frecuencia es de 50 [Hz]
Incógnita
Debemos averiguar cual es el valor de la impedancia y sus componentes
Primer paso – Obtener valores de tensión y corriente
De los datos facilitados debemos primero pasar la tensión y corriente a valores eficaces en forma polar.
Vemos que tanto (230·√2) como (15·√2) son los valores de pico de la señal de tensión y corriente respectivamente.
Sabiendo que el valor eficaz es igual a el valor de pico entre √2, nos queda que el valor eficaz de la tensión y de corriente serán de 230 V y 15 A


quedando en forma polar como:
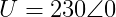

Fíjate en el ángulo. De las funciones de la tensión y corriente obtenemos que el ángulo de la tensión es 0º y el de la corriente es de -60º.
Si te lía lo de forma polar, lo explico en este otro artículo.
Segundo paso – Calcular la impedancia
Aquí simplemente debemos aplicar la ley de Ohm, donde sabemos que U = Z·I, despejando la impedancia Z nos queda que Z = U/I
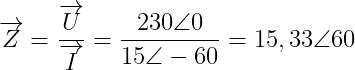
Por tanto ya tenemos la respuesta a la primera incógnita, el valor de la impedancia será de 15,33 ∠60º Ω.
Tercer paso – Componentes de la impedancia
Ahora solo debemos descomponer el fasor de la impedancia de forma polar a forma cartesiana. La componente real o resistiva y la componente imaginaria o reactiva.

por tanto la componente resistiva será de 7,66 Ω
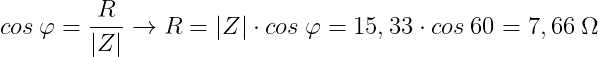
y la componente reactiva será de 13,279 Ω

al ser el fasor de corriente retrasado al fasor de la tensión, esta componente reactiva será inductiva. De aquí podemos calcular el valor de inductancia sabiendo que XL=2πf·L