Aunque no era la intención inicial de este blog, un gran número de preguntas y consultas que recibo son sobre cálculo de potencias por parte de estudiantes de electrotécnica, y que tienen dudas a la hora de afrontar los cálculos, sobretodo fasoriales.
En este post recogeré varios conceptos necesarios para hacer al calculo de potencias en corriente alterna.
Tabla de contenido
Números complejos y fasores
Para el calculo de potencias o cualquier calculo con fasores utilizamos los números complejos.
Los números complejos los podemos dividir en dos componentes, los números reales (eje de abscisas) y los números imaginarios (eje de ordenadas), siendo estos últimos la raíz cuadrada de un número real negativo.
En electrotécnica la componente imaginaria se representa como j que es igual a √-1. Por tanto, √ -25 es igual a j√25 = j5, y asi con culaquier otro número.
Un número complejo X lo podemos expresar como X = a + jb, siendo «a» la componente real y «jb» la componente imaginaria.
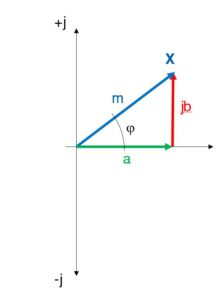
El número complejo X forma un fasor con origen de coordenadas (0,0) hasta su extremo (a,b).
Partes de un fasor
Todo fasor o magnitud fasorial la podemos descomponer en 4 partes:
- Dirección: recta sobre la que se traza el fasor. Para poner un símil, es como una calle recta.
- Sentido: indica uno de los dos sentidos que puede tener el fasor sobre la recta. Es como una calle, vas en un sentido u otro.
- Modulo: es la «longitud» del fasor de la magnitud que representa. Es como la fuerza en que lanzas los pájaros de Angry Birds.
- Ángulo: Es el angulo del fasor respecto al eje de coordenadas. Es como el angulo que escoges al lanzar los pájaros de Angry Birds.

Para obtener el modulo «m» solo tenemos que aplicar el teorema de Pitágoras:

Y para calcular el angulo o argumento aplicamos la siguiente expresión:

Notación de los fasores
Los fasores se pueden escribir de diferentes formas, siendo cada una de las notaciones más apropiada según el tipo de operación que vayamos a realizar.
Estas notaciones son las más habituales:
| Binómica | Se utiliza para sumar y restar fasores | |
| Polar | Se utiliza para multiplicar o dividir fasores |
Conjugado de un fasor
Un fasor conjugado es el mismo fasor pero desplazado de forma simétrica al eje de abscisas.

En otras palabras, si un fasor X en notación binómica es igual a a+jb, su conjugado será a-jb. De igual forma en notación polar, el modulo será el mismo, pero el angulo φ cambia de signo (- φ ).
El fasor conjugado se expresa con un asterisco (X*)
Cálculo de las potencias
Empezaremos con el calculo de:
- Potencia aparente (S)
- Potencia activa y reactiva (P y Q)
Potencia aparente
Podemos definir la potencia aparente como la potencia total demanda por las cargas, y que por tanto el sistema de distribución deberá transportar. Se mide en voltiamperios [VA].
También es puede definir como el módulo de la potencia compleja, cuyo cálculo vectorial es igual a

donde
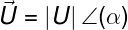
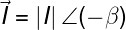
por tanto el conjugado del fasor corriente será

dando como resultado de la potencia compleja
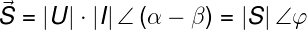
Potencia activa y reactiva
Como hemos visto antes un fasor lo podemos representar en varias notaciones. Si expresamos el fasor de la potencia compleja en notación binómica obtenemos

donde P es la potencia actíva, medida en vátios [W] y Q es la potencia reactiva, medida en voltiamperios reactivos [var].
A partir de aquí simplemente aplicamos las nociones de números complejos que vimos anteriormente, y aplicamos conceptos básicos de trigonometría.


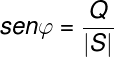
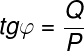
Potencia en R, L y C
Para cualquier impedancia «Z», la potencia compleja absorbida será S = P+jQ. Ahora bien, según el tipo de carga puede ser que tenga un consumo solo de potencia activa, solo de reactiva o de ambos.
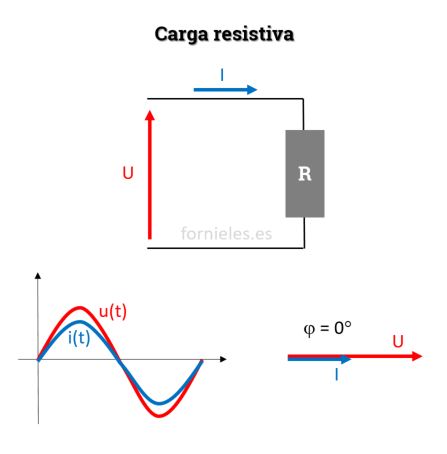
Carga resistiva
En una carga resistiva tenemos el fasor tensión y corriente en fase, con lo que el angulo entre ellos será cero. Por tanto, la potencia absorbida será S=P, solo tendremos potencia activa (P) y la potencia reactiva (Q) será nula.

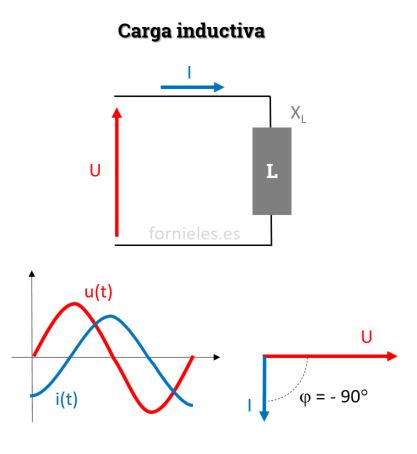
Carga inductiva
En una carga inductiva tenemos el fasor corriente retrasado -90º. Por tanto, la potencia absorbida será S=jQ, solo tendremos potencia reactiva (Q) con un angulo de +90º y la potencia activa (P) será nula.

Carga capacitiva
En una carga capacitiva tenemos el fasor corriente adelantado +90º. Por tanto, la potencia absorbida será S=-jQ, solo tendremos potencia reactiva (Q) con un angulo de -90º y la potencia activa (P) será nula.


Triangulo de potencias
Al final acabamos obtenemos un triangulo de potencias cuando combinamos cargas RLC.
Si el sistema esta compuesto con cargas resistivas y predominantemente inductivas el triangulo resultante será de esta forma

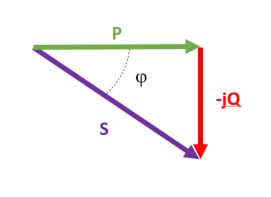
Si el sistema esta compuesto con cargas resistivas y predominantemente capacitivas el triangulo resultante será de esta forma
Cuadrantes de las potencias
El fasor de la potencia compleja o aparente puede encontrase en cuatro cuadrantes en funcion de cual sea el flujo de dicha potencia.
Según las normas IEC 60375 e IEC 61557-12, la potencia puede ser consumida o suministrada.
La potencia activa en los cuadrantes Q1 y Q4 corresponden a consumo, y los cuadrantes Q2 y Q3 corresponde a generación.
Cuando la potencia reactiva tiene el mismo signo que la potencia activa, el sistema es de tipo inductivo. Esto sucede en los cuadrantes Q1 y Q3.
Cuando la potencia reactiva tiene el signo distinto al de la potencia activa, el sistema es de tipo capacitivo. Esto sucede en los cuadrantes Q2 y Q4.

Espero que os sirva de ayuda para los cálculos de potencias.
Photo by Nick Fewings on Unsplash